범주형 자료 - 승산비( 2 x 2 x k )

범주형 자료 - 승산비( 2 x 2 x k )

• 승산비 예 중국 8개 도시마다 폐암환자와 흡연관계를 조사한 자료가 있다. 흡연유무에 따른 폐암환자 승산비는 각 도시마다 동일한지 알아본다. 전체 흡연유무에 따른 폐암환자 승산비는 동일한지도 알아본다. 이 경우 변수가 3개이므로 3차원 표를 만들어야 한다. 

1. 3 차원 승산비는 그림에서 "분석->기술통계량->교차분석" 메뉴를 선택한다. 아래의 그림에는 freq 변수에 가중치가 적용되어 있다. 승산비 검정에 사용하는 자료가 여기에 있다. 승산비는 위험도(relative risk)와 함께 제공되며 "통계량->위험도" 메뉴를 선택하여 구한다. 

2. 통계량 창에서

• "카이제곱"
• "위험도"
• "Cochran 및 Mantel-Haenszel 통계량"

을 선택하고, 셀 출력 창에서 "관측빈도, 행, 열, 전체"를 선택하고 "계속" 버튼을 버튼을 클릭한다.

3. 각 도시에 대한 분할표와 카이제곱 검정결과  

 3-1. 각 도시별 빈도표

3-2. 각 도시별 카이제곱 검정 결과

3-3. 각 도시별 승산비(odds ratio)와 위험도(relative risk)

 3-4. 각 도시마다 승산비가 동일한지 검정과 조건부 동립성 그리고 공통승산비

범주형 자료 - 승산비( 2 x 2)

범주형 자료 - 승산비( 2 x 2)

• 승산비 예 남녀별 음주에 대한 승산비는 같은지 알아보자.

1. 승산비는 그림에서 "분석->기술통계량->교차분석" 메뉴를 선택한다. 아래의 그림과 같이 변수가 저장되어 있다면 빈도 변수에 가중치를 적용한 후 분석을 실시해야 한다. 변수에 가중치 적용은 적합도 검정을 참고 한다. 검정에 사용하는 자료가 여기에 있다. 승산비는 위험도(relative risk)와 함께 제공되며 "통계량->위험도" 메뉴를 선택하여 구한다. 

2. 승산비의 추정값은 9.333이고 95% 신뢰구간은 하한값 4.870에서 상한값 17.886이다. 신뢰구간에 1이 포함되어 있지 않으므로 남자 승산(odds)이 여자 승산(odds)보다 크다고 할 수 있다. 통계적으로 성별에 따른 오락물 방영에 대한 의견은 서로 독립이다.

범주형 자료 - 독립성 검정

범주형 자료 - 독립성 검정(independence test)

• 독립성 검정 예 텔레비젼에서 방송되는 오락물에 대한 사람들의 의견이 성별과 어떤 관계가 있는지 조사하기 위해서 1250명의 사람을 임의추출하여 성별과 오락물 방영에 대한 의견을 조사하였다. 이 자료로 독립성 검정(independence test)을 실시해 보자. 

1. 독립성 검정은 그림에서와 같이 "분석->기술통계량->교차분석" 메뉴를 선택한다. 아래의 그림과 같이 변수가 저장되어 있다면 관측값 변수에 가중치를 적용하여 독립성 분석을 실시해야 한다. 변수에 가중치 적용은 아래 그림과 같이 한다. 검정에 사용하는 자료가 여기에 있다. 

2. 가중치 적용 

아래의 그림과 같이 변수가 저장되어 있다면 관측값 변수에 가중치를 적용하여 독립성 검정을 실시해야 한다. 가중치 적용은

1. "데이터->가중 케이스" 메뉴를 선택하고
2. "가중 케이스 창"에서 "관측값" 변수를 "가중케이스 지정"의 "빈도변수"에 추가한다.

3. 교차 분석 창에서 "행"에 "성별" 변수를 "열"에 "오락물방영" 변수를 입력한다. 그리고 "통계량" 버튼과 "셀" 버튼를 클릭하여 여러가지 출력을 선택한다.
 

4. 통계량 창에서 "카이제곱"을 선택하고 셀 출력 창에서 "관측빈도, 행, 열, 전체"를 선택하고 "계속" 버튼을 버튼을 클릭한다.

5.  셀 출력 창의 빈도 항목에서 "관측빈도", 퍼센트 항목에서 "행", "열", "전체"를 선택한다. 

6. 독립성 검정에 대한 검정결과가 출력되며 Pearson 카이제곱의 점근 유의확률이 0.200이므로 통계적으로 성별에 따른 오락물 방영에 대한 의견은 서로 독립이다. 

범주형 자료 - 동질성 검정

범주형 자료 - 동질성 검정(homogeneity test)

• 동질성 검정 예 두 가지 식이요법 A, B의 효과를 비교하기 위하여 150명의 환자를 대상으로 조사를 실시하였다. 임의로 추출된 80명에게는 식이요법 A를 적용하고, 나머지 70 명에게는 식이요법 B를 적용한 후 얼마간의 시간이 흐른 후에 각 환자의 건강상태에 따라 세 가지 범주로 구분하였다. 이 자료로 동질성 검정(homogeneity test)을 실시해 보자. 

1. 동질성 검정은 그림에서와 같이 "분석->기술통계량->교차분석" 메뉴를 선택한다. 아래의 그림과 같이 변수가 저장되어 있다면 관측값 변수에 가중치를 적용하여 동질성 분석을 실시해야 한다. 변수에 가중치를 적용하는 방법은 다음 화면에 있다. 검정에 사용하는 자료가 여기에 있다. 

2. 아래의 그림과 같이 변수가 저장되어 있다면 관측값 변수에 가중치를 적용하여 동질성 검정을 실시해야 한다. 가중치 적용은

1. "데이터->가중 케이스" 메뉴를 선택하고
2. "가중 케이스 창"에서 "관측값" 변수를 "가중케이스 지정"의 "빈도변수"에 추가한다

3. 교차 분석 창에서 "행"에 "유전종류" 변수를 "열"에 "건강상태" 변수를 입력한다. 그리고 "통계량" 버튼과 "셀" 버튼를 클릭하여 여러가지 출력을 선택한다. 

4. 통계량 창에서 "카이제곱"을 선택하고 셀 출력 창에서 "관측빈도, 행, 열, 전체"를 선택하고 "계속" 버튼을 버튼을 클릭한다.

5. 셀 출력 창의 빈도 항목에서 "관측빈도", 퍼센트 항목에서 "행", "열", "전체"를 선택한다. 

6. 동질성 검정에 대한 검정결과가 출력되며 Pearson 카이제곱의 점근 유의확률이 0.016이므로 통계적으로 건강상태에 따른 유전종류의 비율이 모두 같지 않다고 할 수 있다. 

범주형 자료 - 적합도 검정

범주형 자료 - 적합도 검정

• 적합도 검정 예 어떤 나무의 자가수정의 결과로 나올 수 있는 유전자의 형태는 세 종류로 분류된다고 한다. 이 세 종류를 각각 A, B, C라 할 때 생물학에서의 한 이론에 의하면 비율이 1 : 2 : 1로 나타난다고 하자. 이를 입증하기 위하여 자가수정의 결과로 생겨난 나무 100 그루를 유전자의 형태별로 분류하였다. 이 자료로 적합도 검정(goodness-of-fit test)을 실시해 보자. 

1. 적합도 검정은 그림에서와 같이 "분석->비모수 검정->레거시 대화 상자->카이제곱" 메뉴를 선택한다. 검정에 사용하는 자료가 여기에 있다.  

2. 자료에 가중치 주기

아래 그림은 원자료(raw data)가 아니고 요약된 자료가 저장되어 있다. 이런 경우는 적합도 검정을 실행하기 전 관측값 변수에 가중치를 적용하고 적합도 검정을 실시해야 한다. 가중치 적용은

1. "데이터->가중 케이스" 메뉴를 또는 표준메뉴에서 가중케이스 버튼를 선택
2. "가중 케이스 창"에서 "관측값" 변수를 "가중케이스 지정"의 "빈도변수"에 추가한다 

예를 들어 가중치를 적용하지 않으면 각 변수에 입력값은 18, 55, 27 숫자이나 가중치 적용시 18개, 55개, 27개로 된다.

3. "카이제곱 검정"은 검정변수에 검정할 내용에 대한 변수를 선택하여 입력하고 "기대값"의 "값"에는 검정변수의 기대값 또는 비율을 입력한다.  

4. 적합도 검정에 대한 검정결과가 출력되며 카이제곱의 근사 유의확률이 0.270으로 유전비율은 1:2:1이라고 할 수 있다. 

공분산 분석

공분산분석(Analysis Of COvariance)

• 공분산분석 예 나병환자의 치료법을 연구하기 위하여 A, D 두 항생제의 효과를 비교하려고 한다. 실험에 참여하는 나병환자를 랜덤하게 30명을 뽑은 후 10명에게는 항생제 A, 10명에게는 항생제 D, 나머지 10명 대조군에게는 생리식염수를 투여하고 그 경과를 관찰하였다. 또한 추가로 치료전과 치료후 나병균의 수도 조사하였다.

1. 공분산분석(analysis of covariance)은 그림에서와 같이 "분석->일반선형모형->일변량" 메뉴를 선택한다.

• 종속변수에 치료후 변수 추가
• 모수요인에 항생제 변수 추가
• 공변량 치료전 변수 추가

검정에 사용하는 자료가 여기에 있다. 

2. 각 변수와 교호작용을 모형에 추가한다.

3. 옵션에서 다음 그림과 같이 선택한다.

4. 기술통계량 출력결과

5. 개체-내 효과 검정과 개체-내 대비 검정 결과 : 교호작용은 유의하지 않으므로 분석에서 제외함. 만일 교호작용이 존재하면 공분산분석은 의미없음.

6. 각 변수만 모형에 추가하고 교호작용은 모형에서 제외한다.

7. 평균 비교는 옵션에서 다음 그림과 같이 선택한다.

8. 개체-내 효과 검정(Type III Sum of Squares) 출력결과

9. 모수 추정값 출력결과

10. 공변량과 종속변수 기술 통계량 출력결과와 종속변수 추정값

11. 집단별 평균 차이 검정 결과

회귀분석 - 고급

올리는 중

회귀분석 - 기초

올리는 중

평균 비교에 대한 검정 - 이원배치

평균 비교에 대한 검정 - 이원배치

• 분산 분석 - 이원배치 예제 어느 판유리를 만드는 회사에서 제조시 온도와 판유리 종류별로 유리의 강도에 차이가 있는지를 조사하기 위하여 세 종류의 판우리에 온도를 100도, 125도, 150도에서 반복 각 3회로 27회를 임의로 실험을 실시하여 유리의 강도를 측정한 결과 다음과 같은 데이터를 얻었다. 이 자료에 대한 이원배치 분산분석을 실시해 보자.

이원배치 분산분석 (two - way analysis of variance)

1. 이원배치 분산분석 (two - way analysis of variance)에 대한 검정은 그림에서와 같이 "분석->일반선형모형->일변량" 메뉴를 선택한다. 검정에 사용하는 자료가 여기에 있다. 

2. 검정에 사용할 변수 중

• "종속변수"에 "유리강도"변수를 입력하고
• "모수요인"에 "유리종류, 온도"를 입력하여

이원배치 분산분석을 실행할 수 있다.
세부적인 설정은 "모형", "대비", "도표", "사후분석", "옵션" 버튼을 클릭한다.
다음 화면은 "모형" 버튼을 클릭한 화면이다.

3.  모형 버튼을 클릭하면 현재와 같은 화면이 나타난다.

• 완전요인모형은 완전모형으로 모든 변수와 교호작용을 추가한 모델이고
• 사용자정의는 사용자가 직접 모형을 설정하는 것으로 사용자가 원하는 변수를 모델체 추가하여 분석을 한다.

아래 화면에서는 두 개 요인과 교호작용을 모델에 추가하였다. 다음 화면은 도표 버튼을 클릭한 화면이다.

4.  수정모형, 절편, 유리종류, 온도, 유리종류 *온도 등 모든 변수가 통계적으로 유의하게 나타났다.

5. Plots 버튼을 클릭하면 교호작용을 표로 볼 수 있으며 설정은 다음과 같다.

• 요인에서 가로 축에 사용할 변수 유리종류를 수평축 변수에 입력하고
• 요인에서 그룹으로 묶어 선으로 표현할 변수 온도를 선구분 변수에 입력한다.
• 추가 버튼을 클릭하여 도표를 그릴 설정을 완료한다.

다음 화면은 사후분석 버튼을 클릭하여 평균이 다른 집단이 존재하는지 설정하는 화면이다

6. 도표 출력결과 유리종류와 온도에 대한 유리강도의 평균을 출력한 결과이다. 그래프가 교차하는 것은 교호작용이 있음을 의미한다.

7. Post Hoc 버튼을 클릭하면 사후검정 아래와 같이 설정할 수 있다.

• 요인에서 사후검정에 사용할 변수를 선택하여 사후검정변수에 유리종류, 온도 변수를 추가한다.
• 등분산을 가정함은 등분산이 가정되었을 경우 사후검정방법을 선택하고
• 등분산을 가정하지 않음는 등분산을 가정할 수 없는 경우 사후검정방법을 선택한다.

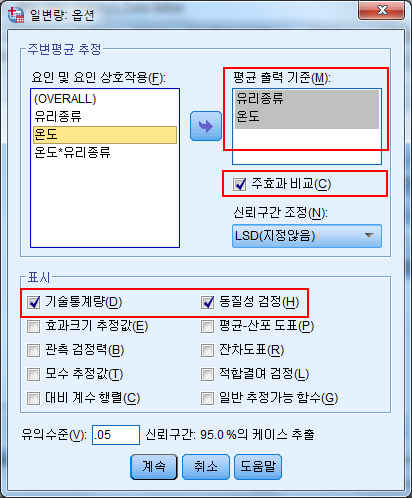
다음 화면은 옵션 버튼을 클릭한 화면으로 주변평균(marginal mean)을 구하는 경우에 사용한다.

8. 앞에서 어떤 모든 변수가 통계적으로 의미있는 결과이었으므로 사후분석을 통하여 각 요인의 어떤 그룹이 다른지 알아보았다. Scheffe, LSD로 분석한 결과 유리종류는 모든 그룹에서 평균이 모두 다르다고 나타났다. 나머지 분석결과는 생략

9. 옵션 버튼을 클릭한 화면으로 주변평균(marginal mean)을 구하는 경우에 사용한다.
 

10. 기술통계량, 오차 분산의 동질성 검정결과 분산이 통계적으로 같다고(유의확률 0.221) 할 수 있다.

11. 모든 설정을 마쳤으면 확인 버튼을 클릭하여 출력결과를 얻는다. 

평균 비교에 대한 검정 - 일원배치

평균 비교에 대한 검정 - 일원배치

• 분산 분석 - 일원배치 예 어느 판유리를 만드는 회사에서 제조시 온도와 판유리 종류별로 유리의 강도에 차이가 있는지를 조사하기 위하여 세 종류의 판우리에 온도를 100도, 125도, 150도에서 반복 각 3회로 27회를 임의로 실험을 실시하여 유리의 강도를 측정한 결과 다음과 같은 데이터를 얻었다. 유리 종류별 강도에 차이가 있는지 일원배치 분산분석을 실시해 보자. 또한 온도별 유리강도의 차이가 있는지 일원배치 분산분석을 실시해 보자. 각 요인에 대한 평균이 차이가 있다고 할 수 있는가? 

1. 일원배치 분산분석(one - way analysis of variance)에 대한 검정은 그림에서와 같이 "분석->평균 비교->일원배치 분산분석" 메뉴를 선택한다. 검정에 사용하는 자료가 여기에 있다. 또 다른 자료도 여기에 있다. 

2. 모든 집단의 분산이 같은 경우

검정에 사용할 두 변수를 선택하여 "종속변수"에 "유리강도"변수를 입력하고 "요인"에 "유리종류"를 입력하여 일원배치 분산분석을 실행한다. 옵션 버튼을 누르고 기술통계, 분산 동질성 검정, Welch를 선택하고 확인 버튼을 클릭한다.

옵션에서

• 기술통계 : 평균을 비교하려고 입력한 요인의 각 그룹마다 평균, 분산, 표준오차 등 기초통계량 출력
• 분산 동질성 검정 : 요인의 각 그룹마다 평균이 같은지 검정한다.
  • 검정결과 요인의 각 그룹마다 분산이 같다면 분산분석으로 각 요인의 그룹별 평균을 비교하고
  • 검정결과 요인의 각 그룹마다 분산이 다르다면 Welch로 각 요인의 그룹별 평균 비교한다.
• Welch : 검정결과 요인의 각 그룹마다 분산이 다를 때 각 요인의 그룹별 평균비교

이다.

3.  요인의 각 그룹간 등분산성 검정결과 유의확률이 0.206으로 요인의 각 그룹간 평균비교는 분산분석으로 검정한다. 평균 비교에 대한 검정 결과 유의확률이 0.462로 모든 집단의 평균은 통계적으로 모두 같다고 할 수 있다. 그리고 여기서 분산분석을 종료한다.

4. 적어도 한 집단의 분산이 다른 것이 존재할 때

검정에 사용할 두 변수를 선택하여 "종속변수"에 "유리강도"변수를 입력하고 "요인"에 "온도"를 입력하여 일원배치 분산분석을 실행한다. 옵션 버튼을 누르고 기술통계, 분산 동질성 검정, Welch를 선택하고 확인 버튼을 클릭한다.
 

5. 요인의 각 그룹간 등분산성 검정결과 유의확률이 0.000으로 요인의 각 그룹간 평균비교는 Welch로 검정한다. 평균 비교에 대한 검정 결과 유의확률이 0.000으로 요인별 각 집단 평균은 통계적으로 다른 집단이 적어도 한 개 있다고 할 수 있다. 이후 어떤 집단의 평균이 다른지 사후검정을 실시하여 알아볼 수 있다. 

6. 검정결과 요인의 각 그룹별 평균이 다르다면 어떤 그룹이 다른지 알아보기 위하여 사후분석(post hoc))을 실시한다.

• 그룹간 등분산을 가정하는 경우에 다중비교방법
• 그룹간 등분산을 가정하지 않는 경우의 다중비교방법에서 선택하고 유의수준을 입력한다.

전 화면에서 결과가 그룹간 등분산을 가정하지 않는 경우이었으므로 Tamhane의 T2 방법을 선택하였다.

7. 등분산을 가정하지 않은 경우 2 집단씩 비교하는 사후검정 결과이다. 출력결과 평균차에 별표(*, asterisk)가 붙은 것은 전 화면에서 설정한 유의수준 0.05 조건하에 평균차이가 통계적으로 있는 것이다. 또한 평균차이가 존재하는 집단들은 유의수준 > 유의확률 관계이다. 

8. 분석결과 실시한 결과 평균차이가 있다고 포함된 것들을 두 그룹으로 나누어 분석하는 방법으로 대비(contrast)를 하기 위한 설정이다. 계수는 한 그룹과 나머지 한 그룹의 계수의 합이 0이 되도록 각 계수를 입력한다.아래 설정화면은

• 첫 번째 그룹 : 온도1(계수 2)
• 두 번째 그룹 : 온도2(계수 -1), 온도3(계수 -1)

로 설정하면 모든 변수에 설정한 계수의 합이 0이 된다. 

9. 대비(contrast) 출력결과 전 화면에서 설정한 대비 계수를 확인할 수 있다.대비검정은 분산분석에서 등분산 검정결과 분산이 같지 않았기에 여기서도 등분산을 가정하지 않습니다인 경우 검정결과 유의확률이 0.000으로 온도1 집단과 온도2, 온도3 집단의 평균은 통계적으로 다르다.